●ピン角の曲げモーメント
ピン角の曲げモーメントMについては、「梁の曲がりの数式表現」で計算したように
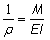 ρ:半径 M:曲げモーメント E:ヤング率 I:断面2次モーメント ρ:半径 M:曲げモーメント E:ヤング率 I:断面2次モーメント
ですので、半径ρを→0にすれば、曲げモーメントMは無限大になります。
(E、及びIは材料・形状から決まる定数)
曲げる場合でなく、曲がりを伸ばすケースでも計算結果は同じです。
又、□要素の上辺が縮み、△要素へ圧縮・変形することを考えてみれば、上辺の真歪(対数歪)が-∞になるので、この要素の歪エネルギーが∞になり、応力が特異点になっていくも分かるでしょう。
他方、視点を変えれば、片持ち梁の完全固定条件も、ピン角条件と考える事もできます。
(もちろん、特異点になるのは力が流れているピン角だけで、例えば、凸部のピン角は力が流れていませんので特異点にはなりません)
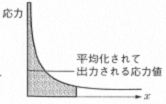
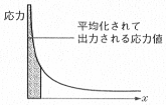
一方、有限要素法では要素内歪みエネルギーを積分して外力の仕事と比較しているので要素内の応力は一旦、平均化されます。
例えとして、関数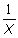 の区間0〜1をガウス積分で積分することを考えます。 の区間0〜1をガウス積分で積分することを考えます。
分割数N=1の積分点は0.211、0.788ですが、10等分した場合の第1区間の積分点は0.021、0.0788となります。区間が1/10になったにも関わらず、この区間の積分値は1分割の10倍にもなります。
結局、表1に示すように要素を細かくするほど要素内の応力は大きくなるのです。
|
|
|
|
|
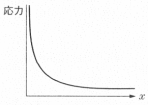
応力分布図
|
大きい要素での出力
|
細かい要素での出力
|
| 表1 |
●有限要素法における適切なサイズ
メッシュを細かくするほど応力が高くなるが、どの程度までメッシュを細かくすれば良いのか?判断に悩む点である。
しかし、実際には「コレ!!」といった手法はないが、よく用いられる例をいくつかを上げる。
どの場合でも、特異点といえるほど(母材の応力の3倍以上に応力が高くなる)、応力値が上昇していることを証明できる程度には
メッシュを分割しておくことが条件である。
・梁の場合の0.3t法

図1
図1の様に、固定端から厚みtの0.3倍の距離の位置の応力を代表応力とする。もちろん、0.3tの箇所の応力の妥当性を検証できるように、前後±0.1t程度に測定点は必要。
図2 推定曲線法
|

|
・推定曲線法
図2のように応力値を距離、応力値でプロットし、直線状態から外れる部分(特異点周辺)を無視して延長し、交点の値を代表値とする。
・要素スキップ
固定端(異常点)の応力を無視する手法で、有限要素法では1要素を飛ばして読み、隣接要素の値を代表応力とする。ただし、荒いメッシュでは応力値が低下し、経験的な判断が必要になる。
細かいメッシュがない場合の推定曲線法の予備的検討に使えます。
●必要な強度
では、このようにして得られた応力値に対して設計強度はどの程度必要なのか?
保証値ではないが、鋼材などでは応力集中係数が大きくなっても切欠き係数が3程度にしかならないことを考慮すると、最低限度、安全率3で設計する必要がある。他の材料も同じような考え方で安全率を考慮すれば問題ないのではないかと思われる。
しかし、最終的には評価試験で確認する事が必要です。
|